DCGAN - Tensorflow 구현, PyTorch 구현
기본적인 개념은 Vanilla GAN과 완전히 똑같고 fully connected layer들을 Conv layer로 바꿔주기만 하면 된다. 그래서 Vanilla GAN을 구현했다면 DCGAN도 쉽게 구현할 수 있다. 다만 Generator에서 transposed convolution이라는 기법을 사용해서 이것만 유의하면 될 것 같다. 논문에는 MNIST에 사용된 DCGAN 구조가 나와있지 않아서 LSUN에 사용된 구조에서 끝 부분만 살짝 변형했다. LSUN 등 3채널 데이터셋에 활용하려면 마지막 출력 부분만 3채널로 바꿔주면 된다.
학습은 i5-6600, GTX 1060(6GB) ubuntu 18.04 환경에서 15분 걸렸다.
기본개념
기본 개념은 GAN과 별 다를게 없으니 전체 모식도와 수식만 후딱 보고 넘어가자. GAN의 기본개념이 잡히지 않았다면 여기를 보고 왔으면 좋겠다.

$$\min_G \max_D V(D, G) = \mathbb{E}_{x \sim p_\text{data}(x)} [\log D(x)] + \mathbb{E}_{z \sim p_g(z)} [\log (1 - D(G(z))]$$
위 식을 최적화시키는 최적의 생성기 $G^*$를 찾는 것이 우리의 목표이다.
Transposed Convolution
이 모델을 구현하는 데에 핵심이라 할 수 있는 기법이다. 일반적인 convolution과 반대로 연산을 하면 이미지가 커진다. 특히 stride를 s를 주면 input보다 s배 큰 feature map을 얻을 수 있다. 왜 이 기법의 이름이 transposed인지, 왜 transposed를 사용 했는지 궁금할 것이다. 하지만 내용이 조금 길어서 시각화와 함께 글을 쓰는 중이다.
구조
위에서 말했다시피 LSUN에 사용된 구조의 출력 부분만 수정했다. G의 마지막 층과 D의 첫 번째 층에 BN을 사용하지 않은 것을 주목하자. 이유는 모르겠지만 이 두 층에 BN을 사용하지 않은 것이 효과가 더 좋다!
그리고 최근 GAN 계열 sota 논문들의 동향을 살펴봤을 때 G와 D가 대칭을 이루는 것도 하나의 특징이라 할 수 있겠다.
원래 MNIST 이미지의 크기는 28 x 28 이지만 64 x 64 로 resize 해서 넣었다. 크기는 네 배 이상 커졌지만 학습은 잘 된다.
| Layer | Discriminator | Generator |
| input | 64 x 64 x 1 | 1 x 1 x 100 |
| 1 | 4 x 4 / 2 (32 x 32 x 128), LReLU | 4 x 4 / 1 (4 x 4 x 1024), BN, ReLU |
| 2 | 4 x 4 / 2 (16 x 16 x 256), BN, LReLU | 4 x 4 / 2 (8 x 8 x 512), BN, ReLU |
| 3 | 4 x 4 / 2 (8 x 8 x 512), BN, LReLU | 4 x 4 / 2 (16 x 16 x 256), BN, ReLU |
| 4 | 4 x 4 / 2 (4 x 4 x 1024), BN, LReLU | 4 x 4 / 2 (32 x 32 x 128), ReLU |
| 5 | 4 x 4 / 1 (1 x 1 x 1), Sigmoid | 4 x 4 / 2 (64 x 64 x 1), tanh |
결과
epoch 1

epoch 20

epoch 1 ~ 20
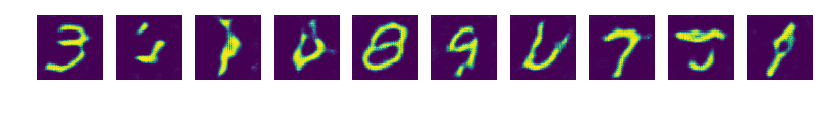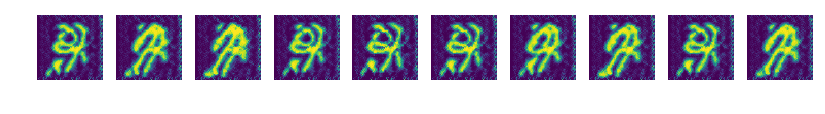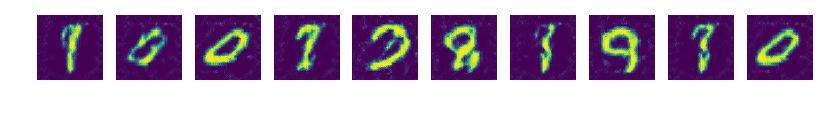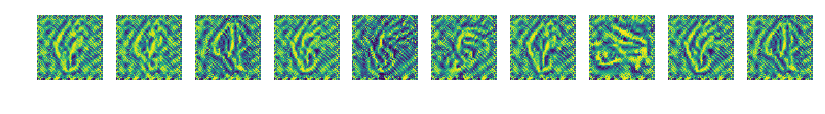
중간에 심각한 mode collapsing이 일어나서 이후 생성물이 망했다.
epoch 6

하지만 이미 1 epoch에서부터 충분히 괜찮은 결과가 보였고 mode collapse 당한 이미지가 더 의미 있을 것 같아서 블로그에 가져왔다.
알게 된 사실들
Latent Vector Interpolation
학습을 성공적으로 시키긴 했어도 이 모델이 의미 있는 이미지를 생성하는 건지 학습하면서 본 이미지들을 외워서 보여주는 건지 알 수가 없다. 하지만 이를 간접적으로 알 수 있는 방법이 있다. $G$의 input인 latent vector $z$를 서서히 변화시켰을 때 생성되는 이미지도 서서히 변한다면 이미지의 semantic한 요소를 어느 정도 학습 했다고 받아 들일 수 있겠다.

그림을 자세히 보면 꽉 막혀 있는 침실에 서서히 대형 창문이 생기는 등 데이터셋의 특징을 잡아내면서 부드럽게 변화하는 것을 볼 수 있다. 영화에서나 잠깐잠깐 보던 영상이라 이 논문을 처음 봤을 당시에는 너무 신기해서 한참 감상했던 기억이 난다.
데이터와 데이터 사이의 빈 공간을 그럴싸한 값으로 채워 넣는 것을 interpolation이라 한다. 이렇게 $G$를 적절히 학습 시키면 latent vector를 서서히 변화시키는 것만으로도 interpolation이 가능하다.
Latent Vector Arithmetic
interpolation 뿐만 아니라 latent vector끼리의 산술 연산도 가능하다.

[웃는 여자 - 무표정의 여자 + 무표정의 남자]를 계산하면 뭐가 나올까? 왠지 [웃는 남자]가 나오지 않을까? 생각한 적이 있을 것이다. 실제로도 그런 것을 확인할 수 있다. 이걸 그냥 무식하게 픽셀 단위로 더하면

의미 없는 이미지들을 얻게 되는데 확실히 $G$가 단순히 이미지를 암기한 것이 아님을 확인할 수 있다. 또, 이걸 변환의 관점에서 생각해 봤을 때 생성기 $G$의 역변환(이 일단 존재한다고 생각하자!)은 각 축이 아무 의미를 가지지 않는 이미지 공간을 어떤 나름의 정돈되고 의미있는 축을 가지는 벡터공간으로 보내는 변환으로 볼 수도 있겠다.
단순한 신경망에서 시작해 점점 더 사람들이 원하는 "인공지능"에 가까워지는 것 같다.
BIAS 외 않써요?
왠지는 잘 모르겠는데 bias를 쓰면 initialize를 어떻게 하건 간에 모델이 걸레짝이 된다.
>> 해답 : BN이 bias를 상쇄시키기 때문이라고 한다. 엄밀히 말하자면 BN안에 bias가 포함되어 있다고 생각하면 되겠다.
tf.layers.conv2d의 Default Initializer
glorot_uniform_initializer(Xavier initializer)라고 한다. 앞으로는 그냥 None으로 놔둬도 될 것 같다.



