MNIST GAN - Git
새벽 두 시가 다 돼가는데 잠이 오질 않는다. 미뤄뒀던 GAN 리뷰나 해봐야겠다.
Generative Adversarial Nets - https://arxiv.org/abs/1406.2661
URL에 써있듯이 2014년 6월에 나온 논문이다. 당시에는 굉장히 혁신적이었지만 지금은 거의 고등학교 미적분 같은 개념이 되어버렸다. 어디서 누가 인공지능으로 사람 목소리, 사람 얼굴 사진, 이모지, 늙어보이는 필터를 만들었다고 하면 거의 이 모델이 기반이 된 것이다.
이전에도 이렇게 학습한 데이터들을 흉내내게 학습하는 모델들이 있었지만 효과는 그리 좋지 않았다. "흉내"를 잘 냈다 못 냈다는 인간이 판단하게 되는데 사람들 맘에 안 들면 거기서 끝인거다.
이 모델의 의의는 생성기 학습을 Adversarial하게 했다는 점과 생성기를 신경망(Net)으로 만들었다는 점이다. 전 세계 딥러닝 전문가들이 극찬했다. 성능을 상당부분 끌어올렸고 급기야 사람 목소리를 흉내내 미용실 예약까지 할 수 있게 된다. 음~ 등의 말 더듬기까지 따라하는 것을 보면 AI라고 믿기 힘들 정도인데 세상에 없는 사람과 통화했다고 생각하면 나 같아도 소름돋을 것 같다. 실제로 통화하신 분은 구글 직원이 가서 말해줄 때까지 AI인 것을 몰랐다고 한다.
급하면 1분 10초부터 보면 된다.
놀라운 건 이 일이 모두 최초의 GAN 논문이 발표되고 4년 안에 일어난 일이라는 것이다. 실제로 2014년에 이 논문이 발표되고 나서, 이 모델에 대한 논문이 기하급수적으로 쏟아지면서 CNN에 이어 딥러닝을 크게 한 번 더 발전시켰다. 14년 6월이면...음...난 고3 기말고사 공부하고 있었다 ㅎㅎ

이 정도면 딥러닝의 한 세부분야를 새로 만들었다고 해도 과언이 아니다. 이 모델에 대해서 알아보자.
개념도
성능은 엄청나지만 최초 Vanilla GAN의 개념은 그렇게 어렵지 않다. 생성기(Generator) $G$와 구분기(Discriminator) $D$를 놓고 서로 경쟁(Adversarial)시키는 것이다.
가장 흔하게 드는 예시가 <경찰과 지폐위조범>이다. 지폐위조범(생성기)는 지폐를 위조하고 경찰(구분기)는 진가를 구분한다. 지폐위조범, 경찰 둘 다 처음엔 미숙해서 성능이 하찮다.
하지만 경찰은 실제 지폐를 보면서 학습하기 때문에 둘을 구분할 수 있게 된다.
지폐위조범은 경찰을 속이기 위해 더 그럴싸하게 만든다. 뒤의 구조도를 보면 알겠지만 생성기는 구분기와 연결되어 있기 때문에 어떻게 해야 구분기가 더 멍청해질 지 예측할 수 있다.
이렇게 서로 경쟁적으로 학습하다보면 나중에는 지폐위조범이 거의 진짜 같이 만들 수 있게 돼 경찰이 웬만해서는 구분하기 힘든 지경에 이른다.
위의 그림에서는 깨끗한 만원 지폐 한 장만 넣어놨지만 실제로는 구겨진 지폐, 낙서된 지폐, 젖은 지폐 등 여러가지 모양의 만원 지폐가 있을 것이다. GAN은 생성기가 다양한 만원짜리를 표현할 수 있도록 학습시킬 수 있다. 그렇다고 데이터를 보고 외워서 출력하진 않는다. 이는 $z$를 interpolation 시킴으로서 증명할 수 있다.
"그럼 생성기는 그냥 깨끗한 만원짜리만 출력해도 되는 것 아닌가??" 하는 의문이 들 수 있다. 충분히 들 수 있는 의문이고 이는 사실 mode collapsing이라 불리며 GAN의 고질적인 문제이다. 뒤의 DCGAN에서 설명하겠다.
이론
우리의 목표는 real data $x$를 이용해 생성기의 분포 $p_g$를 학습시키는 것이다. 이를 위해 생성기의 input이 될 noise $z \sim p_z(z)$를 몇 개 만들고 이를 생성기에 넣어 fake data $G(z;\theta_g)$를 만든다. 구분기는 input $x$가 real data에서 왔을 확률 $D(x;\theta_d)$를 구한다. 전체 모식도를 보면 이렇다.
생성기 $G$와 구분기 $D$의 목표는 서로 상반된다. 생성기는 구분기를 최대한 속이도록 학습해야하고 구분기는 이를 최대한 잘 구분할 수 있도록 학습해야 한다.
다시 말하면, 구분기 $D$는 real data $x \sim p_{\text{data}}(x)$에 대해서는 $\log D(x)$를 최대화해야하고,
$z \sim p_z(z)$에 대해서는 $\log (1 - D(G(z)))$를 최대화 시켜야 한다( $\log D(G(z))$를 최소화 시켜야 한다.)
그리고 생성기 $G$는 $\log (1 - D(G(z)))$를 최소화시켜야 한다.($\log D(G(z))$를 최대화시켜야 한다.)
이렇게 되면, 이 문제는 $G$와 $D$에 대한 minimax game이 된다.
$$\min_G \max_D V(D,G) = \mathbb{E}_{x \sim p_{ \text{data}(x)}}[\log D(x)] + \mathbb{E}_{z \sim p_z(z)} [\log (1 - D(G(z))]$$
Global optimum은 $p_g = p_{\text{data}}$일 때 가진다.
학습
학습은 두 단계로 이루어진다.
1. 생성기의 parameter를 고정시키고 real data와 fake data를 넣어 구분기를 학습시킨다.
2. 구분기의 parameter를 고정시키고 fake data를 구분기에 넣은 값을 이용해 생성기를 학습시킨다.
1. Minibatch 수 만큼 real data와 fake data를 뽑아 구분기를 학습시킨다.
2. Minibatch 수 만큼 fake data를 생성해 생성기를 학습시킨다. 이 때, real data는 생성기에 영향을 주지 않으므로 굳이 넣지 않는다.
학습과정
논문에 실린 그래프인데 GAN의 학습과정을 상당히 잘 보여준다. 여기서 검은 점선은 real data distribtion $p_{\text{data}}$, 초록 실선은 generative distribution $p_g$, 파란 점선은 discriminative distribution을 나타낸다. 그리고 아래 $x$와 $z$는 생성기 $G$가 noise $z$를 data space의 $x$로 mapping하는 것을 나타낸다.
(a) : 맨 처음에는 생성기의 결과가 실제 데이터와 상당히 차이가 많이 나고 구분기 성능도 썩 좋지 않다.
(b) : $G$를 고정하고 $D$를 학습시켜 가짜 데이터를 구분할 수 있게 한다. 이 때, $D_G(x)$는 ${ p_{\text{data}}(x) \over p_{\text{data}}(x) + p_g(x)}$에 가까워진다.
(c) : $D$를 고정하고 $D$의 gradient를 이용해 $G$를 학습시킨다. 생성기는 더 그럴싸한 데이터를 만들 수 있게 된다.
(d) : 위의 (b), (c) 과정을 반복하게 되면 생성기는 완전한 데이터를 만들 수 있게 되고$(p_g = p_{\text{data}})$ 학습이 더 이상 이루어지지 않게 된다. 구분기는 이제 둘을 아예 구분할 수 없어 $D(x) = {1 \over 2}$가 된다.
증명 1. 최적해는 $p_g=p_{\text{data}}$이다.
Proposition 1. 어떤 고정된 $G$에 대하여 최적의 구분기 $D$는 다음과 같다.
증명
$V(G, D)$를 다시 쓰면
$$\begin{align*} V(G, D) &= \int_x p_{\text{data}}(x) \log (D(x))dx + \int_z p_z(z) \log (1 - D(G(z))dz \\ &= \int_x \left [ \, p_{\text{data}}(x) \log (D(x)) + p_g(x) \log (1 - D(x)) \right ]dx \end{align*}$$
가 되는데, $(a, b) \in \mathbb{R}^2 \backslash \{0, 0\}$( $(0, 0)$이 아닌 실수 순서쌍 $(a, b)$ )에 대하여 함수 $ y \rightarrow a \log (y) + b \log (1-y) $가 구간 $[0, 1]$ 안 에서 $y = {a \over a+b}$일 때 최대이므로 $D_G^*(x) = { p_{\text{data}}(x) \over p_{\text{data}}(x) + p_g(x)}$이다.
구분기가 $ Supp (p_{\text{data}}) \cup Supp (p_g) $ 밖에서 정의될 필요는 없으므로 proposition 1.의 증명은 끝난다.
여기서 $Supp$는 "Support"를 뜻하는데, 어떤 함수 $f$에 대하여
$$ Supp(f) = \{ x \in X \,|\, f(x) \neq 0 \} $$
로 정의된다. "$f$가 0이 되지 않게 하는 원소들로 이루어진 $f$의 정의역의 부분집합" 정도로 생각하면 될 것 같다. 그래서 $Supp(p_{\text{data}})$는 data의 범위를 의미한다. $G$가 가질 수 있는 값과 data를 벗어난 값은 구분기에 넣을 일이 없으므로 생각하지 않는다는 뜻이다.
헷갈렸던 것
여기서 좀 헷갈렸던 내용이 있는데, 왜 $D_G^*(x) = { p_{\text{data}}(x) \over p_{\text{data}}(x) + p_g(x)}$냐는 것이다. 분모를 1로 봐서 이해가 잘 되지 않았다. 분모는 1이랑 별로 상관 없다.
마저 증명해보자. 자 이제 위의 식을 이용해 $V(G, D)$를 다시 쓸 수 있다.
$$ \begin{align*} C(G) &= \max_D V(G, D) \\ &= \mathbb{E}_{x \sim p_{\text{data}}} [\log D^*_G(x)] + \mathbb{E}_{z \sim p_z} [\log ( 1 - D^*_G(G(z)))] \\ &= \mathbb{E}_{x \sim p_{\text{data}}} [\log D^*_G(x)] + \mathbb{E}_{x \sim p_g} [\log ( 1- D^*_G(x))] \\ &= \mathbb{E}_{x \sim p_{\text{data}}} \left [\log { p_{ \text{data} }(x) \over p_{ \text{data} }(x) + p_g(x)}\right ] + \mathbb{E}_{x \sim p_g} \left [\log { p_g(x) \over p_{\text{data}}(x) + p_g(x)} \right ] \end{align*}$$
이제 다음 정리를 증명하면 증명이 끝난다.
Theorem 1. $C(G)$가 최소인 것은 $p_g = p_{ \text{data} }$인 것과 동치이다. 그리고 이 때의 $C(G)$는 $-\log4$이다.
증명
$p_g = p_{ \text{data} }$인 $p_g$에 대하여 $D^*_G= {1\over2}$이다. 이를 위 식에 대입하면 $C(G) = \log {1 \over 2} + \log {1 \over 2} = -\log4$가 된다. 이것이 $C(G)$의 최솟값임을 보이자.
$$ \mathbb{E}_{x \sim p_{\text{data}}} [-\log 2] + \mathbb{E}_{x \sim p_g} [- \log 2 ] $$
로부터
$$ \begin{align*} C(G) &= - \log (4) + D_{KL} \left ( p_{\text{data}} \, \Bigg|\Bigg| \, { p_{ \text{data} } + p_g \over 2 } \right ) + D_{KL} \left ( p_g \, \Bigg|\Bigg| \, { p_{\text{data}} + p_g \over 2 } \right ) \\ &= - \log (4) + 2 \cdot JSD ( \, p_{\text{data}} \, || \, p_g \, ) \end{align*} $$
를 얻을 수 있다. Jensen-Shannon divergence는 음수가 아니므로 $C^* = -\log(4)$이고 $p_g = p_{\text{data}}$와 동치이다. 증명 끝.
$\Box$
구현 - Git
전체 코드는 깃에 있다.
위 그림을 보면 구분기의 변수들이 서로 다른 그래프에 중복돼서 사용된다. 이런 경우 reuse=True 해주지 않으면 에러를 낸다.
나머지 부분은 구현이 쉽다.
def discriminator(x, reuse=False):
with tf.variable_scope(name_or_scope='Dis', reuse=reuse):
dw1 = tf.get_variable('w1', [784, 256], initializer=initializer)
db1 = tf.get_variable('b1', [256], initializer=initializer)
dw2 = tf.get_variable('w2', [256, 1], initializer=initializer)
db2 = tf.get_variable('b2', [1], initializer=initializer)
hidden = tf.nn.leaky_relu(tf.matmul(x, dw1) + db1)
output = tf.nn.sigmoid(tf.matmul(hidden, dw2) + db2)
return output
result_of_real = discriminator(X, reuse=True)
결과
epoch 0

epoch 99
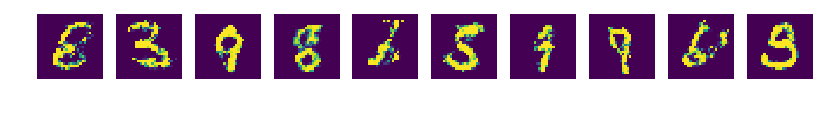
epoch 0~99













