Reference
원문 : https://vincentherrmann.github.io/blog/wasserstein/
Wasserstein GAN and the Kantorovich-Rubinstein Duality
Derivation of the Kantorovich-Rubinstein duality for the use in Wasserstein Generative Adversarial Networks
vincentherrmann.github.io
A Hitchhiker's guide to Wasserstein : http://n.ethz.ch/~gbasso/download/A%20Hitchhikers%20guide%20to%20Wasserstein/A%20Hitchhikers%20guide%20to%20Wasserstein.pdf
Introduction
WGAN 논문에서 EM distance를 계산할 때 Kantorovich-Rubinstein Theorem을 이용해 식을 바로 도출한다. 논문에서는 한 줄만 설명하고 넘겼지만 실제로는 설명할 것이 꽤 많다. Continuous한 방법으로 유도를 하면 복잡한 이론이 많이 쓰여서(Edwards, D. A., On the Kantorovich-Rubinstein Theorem (2011)) 이해할 엄두조차 나지 않는다. 하지만 discrete한 방법으로 최대한 이해하기 쉽게 설명한 게시글이 있어 번역해봤다. 게시글 원저자가 최대한 이해하기 쉽게 설명하느라 엄밀한 설명이 많이 생략되어 있다고 했는데, 중요한 부분마저 생략이 좀 되어 있어서 수식을 하나하나 다 이해해야 되는 사람은 고생을 좀 했을 것이다. 그리고 쉽게 설명하려다가 오히려 더 어려워진 부분도 있어서 읽다가 아쉬웠던 부분은 내가 좀 더 채워 넣었다.
Summary
1. 문제를 discrete한 방법으로 정의를 했다. $\gamma$와 $|| x-y ||$를 행렬 $\mathbf{\Gamma} = \gamma(x, y)$, $\mathbf{D} = ||x - y||$, with $\mathbf{\Gamma}, \mathbf{D} \in \mathbb{R}^{l \times l}$로 정의를 해서 문제를 행렬연산으로 표현을 한다.
2. 그럼 문제가 선형 최적화 문제로 바뀌게 되어 dual form을 이용해 더 쉽게 풀 수 있다.
3. 여기서 duality에 대한 증명을 실어놨다. Weak duality와 Strong duality로 나뉘는데 전자는 한 줄로 쉽게 증명 가능하지만 후자는 Farkas' Lemma가 필요하다. 이 증명들은 이 글을 이해하는 데에 필수적인 건 아니지만 알면 크게 도움된다.
4. 마지막으로 Kantorovich-Rubinstein Theorem(이하 K-R 정리)을 이용하면 WGAN 문제를 1-립쉬츠인 $f$를 이용해 표현 가능해진다.
Earth Mover's Distance
일단 문제의 EMD는 다음과 같이 정의된다.
$$\text{EMD}(P_r, P_\theta) = \inf_{\gamma \in \Pi} \sum_{x, y} ||x - y|| \gamma(x, y) = \inf_{\gamma \in \Pi} \mathbb{E}_{(x, y) \sim \gamma} ||x - y||$$
$\Pi(P_r, P_\theta)$는 $P_r$과 $P_\theta$간의 모든 joint pdf들의 집합이다. 여기서 $\gamma$와 $|| \cdot ||$을 행렬로 표현해보자.
$$\mathbf{\Gamma} = \gamma(x, y), \mathbf{D} = ||x - y||, \text{ with } \mathbf{\Gamma}, \mathbf{D} \in \mathbb{R}^{l \times l}$$
그럼 distance를 $\mathbf{\Gamma}, \mathbf{D}$로 표현이 가능하다.
$$\text{EMD}(P_r, P_\theta) = \inf_{\gamma \in \Pi} \langle \mathbf{D}, \mathbf{\Gamma} \rangle_\mathrm{F}$$
$\langle \cdot, \,\cdot \rangle_\mathrm{F}$는 Frobenius inner product라고 하고 두 행렬의 element-wise곱들의 합을 나타낸다.
Linear Programming
문제와 제한조건(constraints)들을 행렬변환으로 표현할 수 있다면 LP 방법을 사용할 수 있다. LP의 기본적인 형태는 다음과 같다.
$$\newcommand\vec[1]{\mathbf{#1}} \begin{align*} \text{minimize} & \quad z = \vec{c}^T \vec{x}, \,\vec{c} \in \mathbb{R}^n \\ \text{such that}& \quad \vec{Ax} = \vec{b}, \,\vec{A} \in \mathbb{R}^{m \times n}, \,\vec{b} \in \mathbb{R}^m \\ \text{and}& \quad \vec{x} \ge 0 \end{align*}$$
EMD를 찾는 문제를 이 형태로 바꿔주기 위해서 $\mathbf{\Gamma}$와 $\mathbf{D}$를 vectorize시켜준다.
$$\newcommand\vec[1]{\mathbf{#1}} \begin{align*} &\vec{x} = \text{vec}(\vec{\Gamma}) \\ &\vec{c} = \text{vec}(\vec{D}) \end{align*}$$
그럼 $n = l^2$이 된다. 그리고 $\gamma$의 marginal이 $P_r, P_\theta$인 것이 constraint가 된다. 여기서 살짝 잡기술이 필요한데 일단 $\mathbf{b}$를 다음과 같이 정의하면
$$\mathbf{b} = \left [ \begin{array}{c} P_r \\ P_\theta \end{array} \right ]$$
$m = 2l$이 되고, $\mathbf{A}$를 다음과 같이 정의해 constraint $\sum_x \gamma (x, y) = P_r(y), \sum_y \gamma(x, y) = P_\theta(x)$를 $\mathbf{Ax=b}$로 표현할 수 있게 된다.
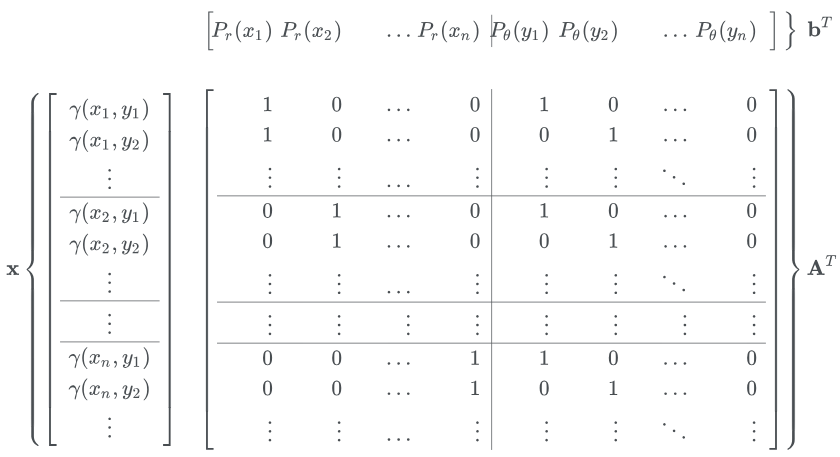
Dual Form
문제를 LP로 표현해놨다고 끝이 아니다. $\gamma$의 marginal들이 가질 수 있는 state는 $n^2$인데 이러면 데이터가 10000개만 돼도 space가 너무 넓어진다.
다행히 우리는 $\gamma$자체가 궁금한게 아니라 EMD를 줄이기만 하면 되기 때문에 문제에 $\gamma$가 등장하지 않게 변형해서 푸는게 가능하다. LP문제는 다음과 같이 멋지게 변형해서 풀 수 있다.
$$\begin{array}{c|c} \mathbf{primal \ form:} & \mathbf{dual \ form:}\\ \begin{array}{rrcl} \mathrm{minimize} \ & z & = & \ \mathbf{c}^T \mathbf{x}, \\ \mathrm{such \ that} \ & \mathbf{A} \mathbf{x} & = & \ \mathbf{b} \\ \mathrm{and}\ & \mathbf{x} & \geq &\ \mathbf{0} \end{array} & \begin{array}{rrcl} \mathrm{maximize} \ & \tilde{z} & = & \ \mathbf{b}^T \mathbf{y}, \\ \mathrm{such \ that} \ & \mathbf{A}^T \mathbf{y} & \leq & \ \mathbf{c} \\ \\ \end{array} \end{array}$$
원 문제를 primal form, 바꾼 문제를 dual form이라 한다. 여기서 이제 두 문제를 푸는 것이 동치임을 증명해야 하는데 일단
$$z = \mathbf{c}^T \mathbf{x} = (\mathbf{c})^T \mathbf{x} \ge (\mathbf{A}^T \mathbf{y})^T \mathbf{x} = \mathbf{y}^T \mathbf{A} \mathbf{x} = \mathbf{y}^T \mathbf{b} = (\mathbf{b}^T \mathbf{y})^T = \tilde{z}$$
임을 이용해 $z$의 lower bound가 $\tilde{z}$임을 보일 수 있다. 이를 Weak Duality라고 한다. $*$를 Optimal solution이라고 할 때 $z \ge z^* = \tilde{z}^* \ge \tilde{z}$임을 보이면 두 form이 동치임이 증명되는데 이는 Strong Duality Theorem을 통해 보일 수 있지만 weak duality에 비해 살짝(많이^^) 복잡하고 Farkas' Lemma가 필요하다. Strong duality 증명 없이도 이 글을 이해할 수 있지만 이 글을 읽으러 온 사람이면 증명을 보고 싶어할 것이라고 생각한다.
Farkas' Lemma
어떤 행렬 $\hat{\mathbf{A}} \in \mathbb{R}^{d \times n}$의 열들을 열벡터 $\mathbf{a}_1, \mathbf{a}_2, \dots \mathbf{a}_n \in \mathbb{R}^d$로 생각할 수 있다. 그러면 이 열벡터들과 음이아닌 계수들로 이루어진 선형조합들은 꼭짓점이 원점인 convex cone을 형성한다. 우린 이 계수들을 $\mathbf{x} \in \mathbb{R}^n_{\ge 0}$으로 표현할 수 있다.
또다른 벡터 $\hat{\mathbf{b}} \in \mathbb{R}^d$는 cone 안에 있거나(경계포함), 밖에 있는 것이 가능하다.
만약 밖에 있다면 $\hat{\mathbf{b}}$와 convex cone 사이를 가로지르고 원점을 지나는 초평면 $h$를 생각할 수 있는데, 이 초평면은 법선벡터 $\hat{\mathbf{y}} \in \mathbb{R}^d$ 하나로 정의할 수 있다. 만약 어떤 벡터 $\mathbf{v} \in \mathbb{R}^d$가 $h$에 포함된다면 $\mathbf{v}^T \hat{\mathbf{y}} = 0$, $\hat{\mathbf{y}}$와 같은 방향에 있다면 $\mathbf{v}^T \hat{\mathbf{y}} > 0$, 반대 방향에 있다면 $\mathbf{v}^T \hat{\mathbf{y}} < 0$이 될 것이다. 만약 $\hat{\mathbf{b}}$가 convex cone 바깥에 있다면 모든 $\mathbf{a}_i$와 $\hat{\mathbf{b}}$를 나누는 초평면 $h$가 존재할 것이다.
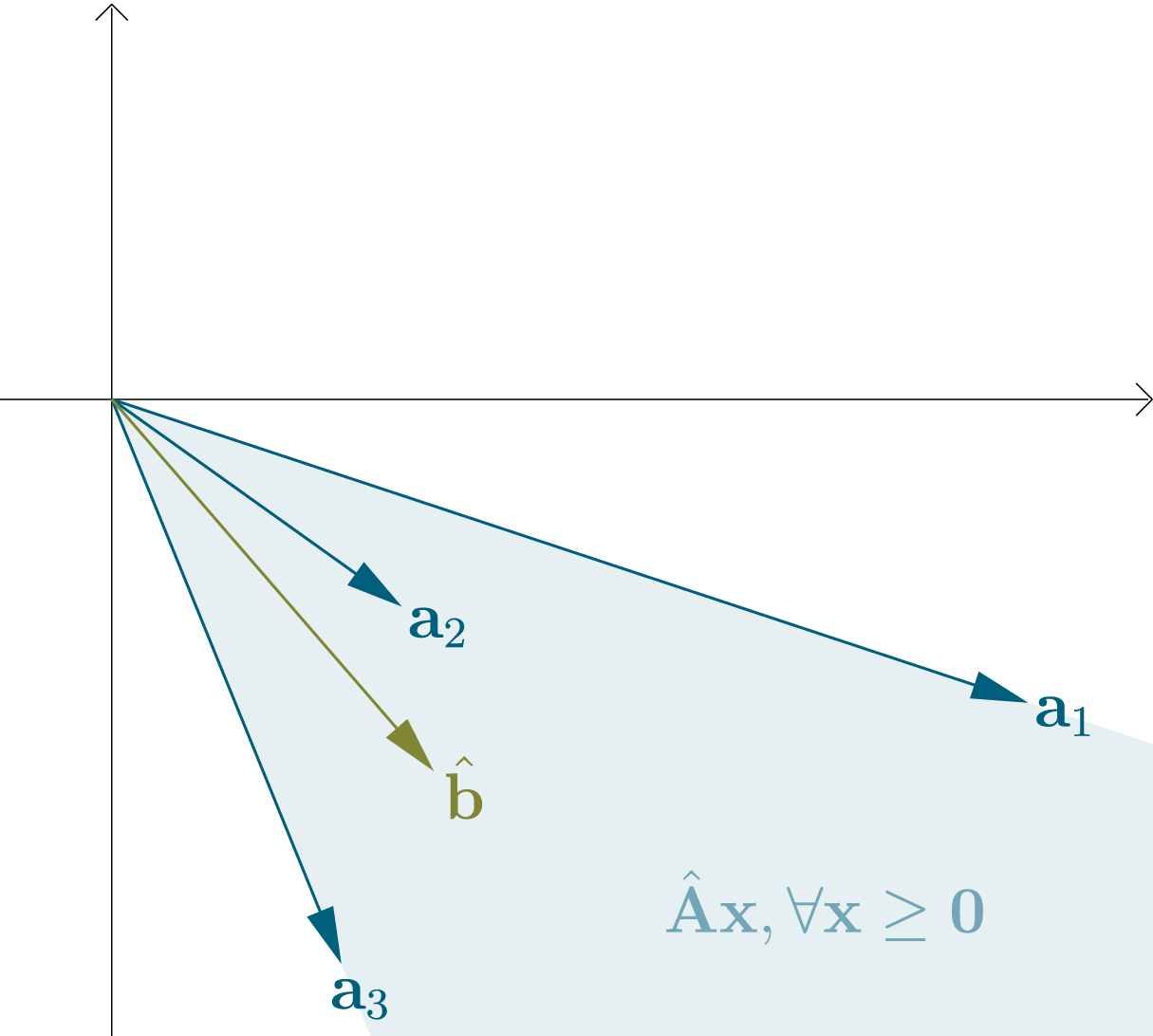
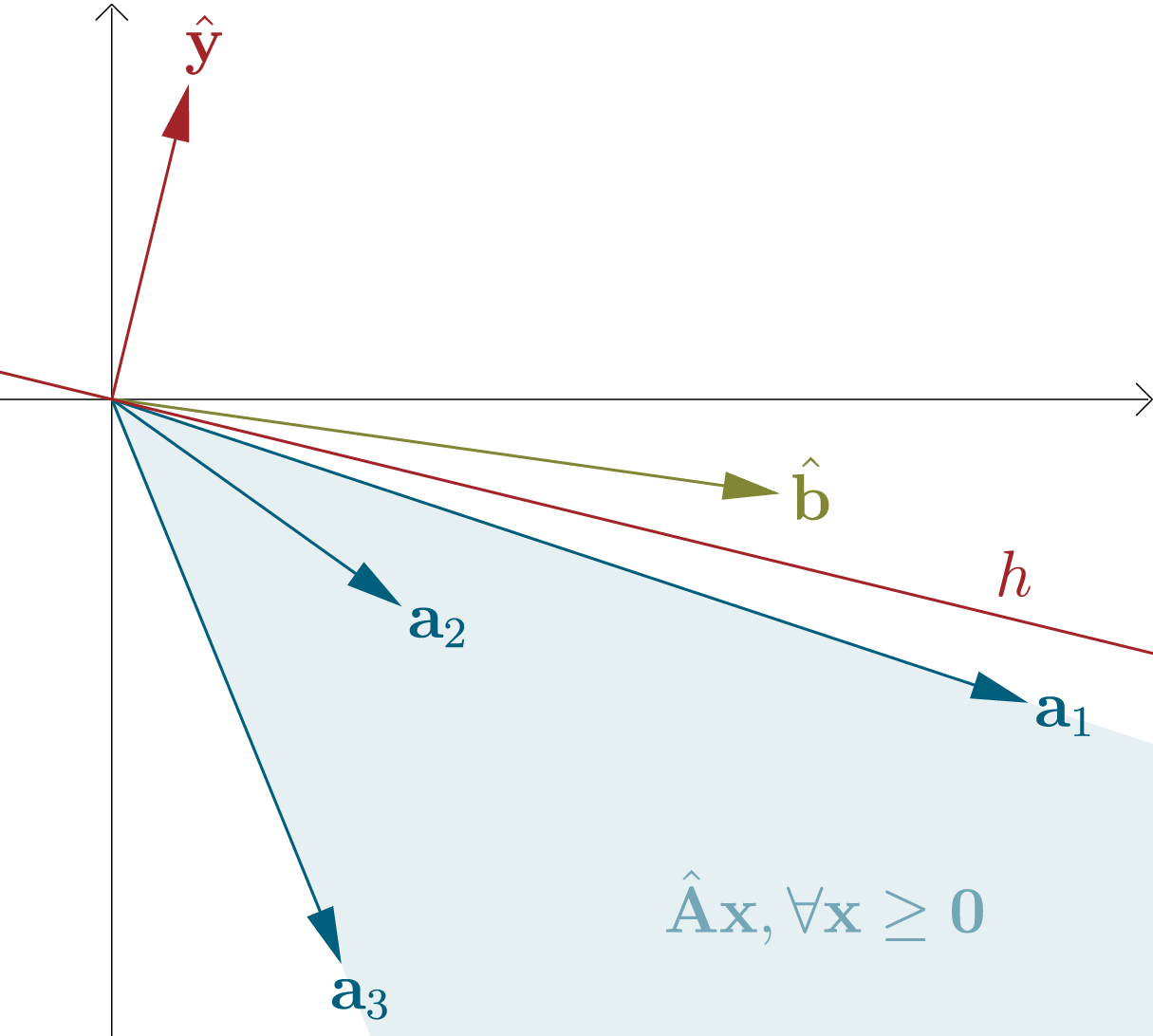
즉, 다음 두 명제 중 무조건 하나만 성립한다.
-
(1) $\hat{\mathbf{A}} \mathbf{x} = \hat{\mathbf{b}}, \mathbf{x} \ge 0$이 되게 하는 $\mathbf{x} \in \mathbb{R}^n$이 존재한다.
-
(2) $\hat{\mathbf{A}}^T \hat{\mathbf{y}} \le 0, \hat{\mathbf{b}}^T \hat{\mathbf{y}} > 0$이 되게 하는 $\hat{\mathbf{y}} \in \mathbb{R}^d$가 존재한다.
+ 만약 $\mathbf{x}$에 음수가 섞여있으면 어떡하지???
그럼 $\text{span} (\hat{\mathbf{A}}) = \mathbb{R}^d$가 되어 (1)이 성립하게 된다.
Farkas' Lemma'
여기부터 이제 원본 글이랑 달라진다. 원본 글의 Strong duality 증명 부분에서 $\alpha$가 등장하는데 항상 $\alpha >0$임을 보이는 부분이 좀 애매해서 그냥 넘기기 너무 힘들었다.(이 글의 strong duality 증명 막바지에 정확한 증명이 나온다.) 그래서 여기부터는 좀 더 정확한 증명을 싣기로 했다. Strong duality를 증명하기 위해선 Farkas' Lemma의 alternative가 필요하다. 보통 Farkas' Lemma'라고 부르던데 여기선 줄여서 Farkas'라고 부르도록 하겠다.
원래의 Farkas와 Farkas'를 연달아 써서 뭐가 다른지 살펴보자.
내가 참조한 자료와 이 게시글의 원문과 부등호 방향이 반대다!! 근데 어차피 말하는 내용은 같으니 duality 증명하는 동안만 부등호를 반대로 써놓자.
Farkas
적당한 행렬과 벡터 $\hat{\mathbf{A}}, \hat{\mathbf{b}}$에 대해 다음 두 명제 중 정확히 (exactly) 한 개만 성립한다.
$$\begin{align*}(1) \ \exists \ \mathbf{x} \in \mathbb{R}^n &\text{ such that } \hat{\mathbf{A}} \mathbf{x} = \hat{\mathbf{b}}, \mathbf{x} \ge 0 \\ (2) \ \exists \ \hat{\mathbf{y}} \in \mathbb{R}^d &\text{ such that } \hat{\mathbf{A}}^T \hat{\mathbf{y}} \ge 0, \hat{\mathbf{b}}^T \hat{\mathbf{y}} < 0\end{align*}$$
Farkas'
적당한 행렬과 벡터 $\hat{\mathbf{A}}, \hat{\mathbf{b}}$에 대해 다음 두 명제(2'와 2''는 동치이다) 중 정확히 한 개만 성립한다.
$$\newcommand\hbf[1]{\hat{\mathbf{#1}}} \begin{align*} (1') \ \exists \ \mathbf{x} \in \mathbb{R}^n &\text{ such that } \hbf{A} \mathbf{x} \le \hbf{b} \\ (2') \ \exists \ \hbf{y} \in \mathbb{R}^d &\text{ such that } \hbf{A}^T \hbf{y} = 0, \hbf{b}^T \hbf{y} < 0, \hbf{y} \ge 0 \\ (2'') \ \exists \ \hbf{y} \in \mathbb{R}^d &\text{ such that } \hbf{A}^T \hbf{y} = 0, \hbf{b}^T \hbf{y} = -1, \hbf{y} \ge 0\end{align*}$$
이제 Farkas'를 증명해보자. 증명은 세 가지 단계로 구성된다.
1. $(2')$와 $(2'')$가 동치임을 보인다.
2. $(1')$과 $(2')$가 동시에 성립할 수 없음을 보인다.
3. $(2')$가 거짓이면 $(1')$이 참임을 보인다.
1. $(2') \Leftrightarrow (2'')$
$(2'') \Rightarrow (2')$인 것은 자명하므로 $(2') \Rightarrow (2'')$인 것만 보이면 된다. $(2')$가 참이라 할 때, $\mathbf{y}' = - {1 \over \hat{\mathbf{y}}^T \hat{\mathbf{b}}} \hat{\mathbf{y}}$라 놓으면 $\hat{\mathbf{y}} \ge 0, \hat{\mathbf{y}}^T \hat{\mathbf{b}} < 0$니까 $\mathbf{y}' \ge 0$일거고
$$\mathbf{y}'^T \hat{\mathbf{b}} = - {\hat{\mathbf{y}}^T \hat{\mathbf{b}} \over \hat{\mathbf{y}}^T \hat{\mathbf{b}}} = -1$$
가 된다. 그리고
$$\hat{\mathbf{A}}^T \tilde{\mathbf{y}} = - {1 \over \hat{\mathbf{y}}^T \hat{\mathbf{b}}} (\hat{\mathbf{A}}^T \hat{\mathbf{y}}) = 0 \qquad (\because \hat{\mathbf{A}}^T \hat{\mathbf{y}} = 0)$$
여서 $(2'')$의 조건을 만족하는 $\mathbf{y}'$가 존재하여 명제가 참이 된다.
2. $(1') \land (2') \text{ is false.}$
$(1'), (2')$둘 다 성립하다고 가정해보자.
$$\newcommand\hbf[1]{\hat{\mathbf{#1}}} \begin{align*} &\hat{\mathbf{y}}^T \hat{\mathbf{A}} \mathbf{x} = \hat{\mathbf{y}}^T ( \hat{\mathbf{A}} \mathbf{x}) \le \hat{\mathbf{y}}^T \hat{\mathbf{b}} \ {\color{red} {< 0}} & (\because \hat{\mathbf{A}} \mathbf{x} \le \hat{\mathbf{b}} \text{ from } (1'), \ \hat{\mathbf{y}}^T \hbf{b} < 0 \text{ from } (2')) \\ &\hbf{y}^T \hbf{A} \mathbf{x} = (\hbf{y}^T \hbf{A}) \mathbf{x} = (\hbf{A}^T \hbf{y})^T \mathbf{x} \ {\color{red} {= 0}} & (\because \hbf{A}^T \hbf{y} = 0 \text{ from } (2'))\end{align*}$$
모순되므로 두 명제는 한 번에 성립할 수 없다.
3. $\neg(2') \Rightarrow (1')$
$\neg (2') \Leftrightarrow \neg(2'')$이므로 $\neg (2'')$가 참이라 가정해보자. 즉,
$$\newcommand\hbf[1]{\hat{\mathbf{#1}}} \nexists \ \hbf{y} \in \mathbb{R}^d, \ \hbf{A}^T \hbf{y} =0, \ \hbf{y}^T \hbf{b} = -1, \ \hbf{y} \ge 0$$
그리고 $\bar{\mathbf{A}} = \left [ \begin{array}{c} \hat{\mathbf{A}}^T \\ \hat{\mathbf{b}}^T \end{array} \right ], \ \bar{\mathbf{b}} = \left [ \begin{array}{c} 0 \\ \vdots \\ 0 \\ -1 \end{array} \right ]$라 놓으면
$$\newcommand\hbf[1]{\hat{\mathbf{#1}}} \bar{\mathbf{A}} \mathbf{z} = \bar{\mathbf{b}}, \mathbf{z} \ge 0 \Leftrightarrow \hbf{A}^T \mathbf{z} = 0, \mathbf{z}^T \hbf{b} =-1, \mathbf{z} \ge 0$$
라서 가정에 의해 $\bar{\mathbf{A}}, \bar{\mathbf{b}}$에 대해 $(1)$이 거짓이므로 $(2)$는 참이 된다. $(\because \text{ Farkas' Lemma})$. 즉,
$$\exists \ \mathbf{s} \in \mathbb{R}^d \text{ such that } \bar{\mathbf{A}}^T \mathbf{s} \ge 0, \ \mathbf{s}^T \bar{\mathbf{b}} < 0$$
(그냥 $(2)$에다가 $\mathbf{s}$ 넣은 식이다.)
가 성립한다. $\mathbf{s} = \left [ \begin{array}{c} \mathbf{x} \\ \lambda \end{array} \right ] \; (\mathbf{x} \in \mathbb{R}^n, \lambda \in \mathbb{R})$로 놓으면
$$\newcommand\hbf[1]{\hat{\mathbf{#1}}} \newcommand\vec[1]{\mathbf{#1}} \newenvironment{mat}[1] {\left [ \begin{array}{#1}} {\end{array} \right ]} \begin{align*} &\bar{\mathbf{b}}^T \mathbf{s} < 0 \Rightarrow \begin{mat}{c} 0 \\ \vdots \\ 0 \\ -1 \end{mat} ^T \begin{mat}{c} \vec{x} \\ \lambda \end{mat} = 0 + (-\lambda) < 0 \Rightarrow \lambda > 0 \\ &\bar{\vec{A}}^T \vec{s} \ge 0 \Rightarrow \begin{mat}{c} \hbf{A}^T \\ \hbf{b}^T \end{mat} \begin{mat}{c} \vec{x} \\ \lambda \end{mat} = \begin{mat}{cc} \hbf{A} & \hbf{b} \end{mat} \begin{mat}{c} \vec{x} \\ \lambda \end{mat} = \hbf{A} \vec{x} + \lambda \hbf{b} \ge 0 \Rightarrow \hbf{A} \vec{x} \ge -\lambda \hbf{b} \Rightarrow \hbf{A} {\color{red} {\left ( - {1 \over \lambda} \vec{x} \right )}} \le \hbf{b} \\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \therefore \exists \ \vec{x}' \text{ such that } \hbf{A} {\color{red} {\vec{x}'}} \le \hbf{b} \end{align*}$$
이므로 $(1')$이 성립한다. 증명 끝!
Strong Duality
드디어 Strong Duality를 증명할 시간이 왔다. 그렇게 어렵지 않다. 학부 수준의 선형대수 산수만 열심히 하면 된다. 문제를 다시 한 번 써보자.
$$\begin{array}{c|c} \mathbf{primal \ form:} & \mathbf{dual \ form:}\\ \begin{array}{rrcl} \mathrm{minimize} \ & z & = & \ \mathbf{c}^T \mathbf{x}, \\ \mathrm{such \ that} \ & \mathbf{A} \mathbf{x} & = & \ \mathbf{b} \\ \mathrm{and}\ & \mathbf{x} & \geq &\ \mathbf{0} \end{array} & \begin{array}{rrcl} \mathrm{maximize} \ & \tilde{z} & = & \ \mathbf{b}^T \mathbf{y}, \\ \mathrm{such \ that} \ & \mathbf{A}^T \mathbf{y} & \leq & \ \mathbf{c} \\ \\ \end{array} \end{array}$$
Strong Duality Theorem
다음 네 명제 중 하나만 성립한다.
Case 1. 둘 다 해가 없다. (Both infeasible)
Case 2. primal이 infeasible하고 dual이 unbounded 된다.
Case 3. dual이 infeasible하고 primal이 unbounded 된다.
Case 4. 둘 다 feasible하고 최적값은 같다.
+ 여기서 infeasible과 unbounded가 좀 헷갈렸었는데, infeasible은 조건을 만족하는 경우가 없는 것을 말하고 unbounded는 object가 발산함을 말한다.
증명을 좀 더 정확히 이해하고 싶다면 위의 Farkas와 Farkas'를 종이에 적어놓고 천천히 따라오는게 좋을 것 같다. 증명 중에 언급할 때마다 무슨 내용인지 써놓고 싶지만 그랬다간 latex 대참사가 일어날 것이다.
우리는 적어도 한 쪽이 feasible한 경우만 생각할거기 때문에 Case 1이 거짓이라고 가정하자.
Case 2. primal이 infeasible하고 dual이 unbounded 된다.
$\bar{\mathbf{y}}$가 dual의 feasible solution이고 primal이 infeasible하다 가정하자. 그럼 $\mathbf{Ax} = \mathbf{b}, \mathbf{x} \ge 0$의 해가 없으므로 $(1)$이 거짓이 되어 $(2)$가 참이 된다. 즉,
$$\newcommand\hbf[1]{\hat{\mathbf{#1}}} \exists \ \hbf{y} \in \mathbb{R}^d \text{ such that } \hbf{A}^T \hbf{y} \ge 0, \hbf{b}^T \hbf{y} < 0.$$
반직선 $\bar{\mathbf{y}} - \lambda \mathbf{y}, \lambda \ge 0$에 대해
$$\mathbf{A}^T (\bar{\mathbf{y}} - \lambda \mathbf{y}) = \mathbf{A}^T \bar{\mathbf{y}} - \lambda \mathbf{A}^T \mathbf{y} \le \mathbf{c}$$
이므로 $\bar{\mathbf{y}} - \lambda \mathbf{y}$ 또한 dual feasible이고
$$\mathbf{b}^T (\bar{\mathbf{y}} - \lambda \mathbf{y}) = \mathbf{b}^T \bar{\mathbf{y}} - \lambda \mathbf{b}^T \mathbf{y}$$
에서 $\mathbf{b}^T \mathbf{y} < 0$이므로 $\lambda \rightarrow \infty$이면 $\mathbf{b}^T (\bar{\mathbf{y}} - \lambda \mathbf{y}) \rightarrow \infty$이 된다.
따라서 dual이 unbounded 된다.
Case 3. dual이 infeasible하고 primal이 unbounded 된다.
Case 2와 비슷하다. $\bar{\mathbf{x}}$가 primal의 feasible solution이고 dual이 infeasible하다 가정해보자. 그럼 $\mathbf{A}^T \mathbf{y} \le \mathbf{c}$의 해가 없으므로 $(1')$이 거짓이 되어 $(2')$가 참이 된다. 그럼 또,
$$\newcommand\hbf[1]{\hat{\mathbf{#1}}} \exists \ \hbf{x} \in \mathbb{R}^n \text{ such that } \hbf{A} \hbf{x} = \mathbf{0}, \mathbf{c}^T \hbf{x} < 0, \hbf{x} \ge 0 \\ ( (2') : \exists \ \hbf{y} \in \mathbb{R}^d \text{ such that } \hbf{A}^T \hbf{y} = \mathbf{0}, \hbf{b}^T \hbf{y} < 0, \hbf{y} \ge \mathbf{0} )$$
가 성립한다. 원래의 $(2')$와 notation만 다를 뿐 똑같은 식이다.
또 이제 반직선 $\bar{\mathbf{x}} + \lambda \mathbf{x}, \lambda \ge 0$에 대해
$$ \mathbf{A}(\bar{\mathbf{x}} + \lambda \mathbf{x}) = \mathbf{A} \bar{\mathbf{x}} + \lambda \mathbf{A} \mathbf{x} = \mathbf{b} + \lambda \cdot \mathbf{0} = \mathbf{b} $$
이므로 $\bar{\mathbf{x}} + \lambda \mathbf{x}$도 primal feasible하다. 그리고,
$$ \mathbf{c}^T (\bar{\mathbf{x}} + \lambda \mathbf{x}) = \mathbf{c}^T \mathbf{x} + \lambda \mathbf{c}^T \mathbf{x}$$
인데, $\mathbf{c}^T \mathbf{x} < 0$이라서 $\lambda \rightarrow \infty$이면 $\mathbf{c}^T (\bar{\mathbf{x}} + \lambda \mathbf{x}) \rightarrow -\infty$이 된다.
따라서 primal이 unbounded 된다.
Case 4. 둘 다 feasible하고 최적값은 같다.
$\bar{\mathbf{x}}, \bar{\mathbf{y}}$를 각각 primal, dual의 feasible solution이라 하면, 아까 Weak Duality에 의해 $\newcommand\bbf[1]{\bar{\mathbf{#1}}} \mathbf{c}^T \bbf{x} \ge \mathbf{b}^T \bbf{y}$여서 서로 bounded된 것을 볼 수 있다. ${z}^*$를 primal의 optimal value로 놓고 dual의 optimal value가 ${z}^*$보다 작다고 가정하면,
$$\mathbf{c}^T \bar{\mathbf{x}} \ge {z}^* > \mathbf{b}^T \bar{\mathbf{y}}$$
가 성립하게 되어 다음의 명제도 성립한다.
$$\begin{align*} &\nexists \ \mathbf{y} \text{ such that } \mathbf{A}^T \mathbf{y} \le \mathbf{c}, \mathbf{b}^T \mathbf{y} \ge {z}^* \\ \Leftrightarrow \ & \nexists \ \mathbf{y} \text{ such that } \left [ \begin{array}{c} \mathbf{A}^T \\ -\mathbf{b}^T \end{array} \right ] \mathbf{y} \le \left [ \begin{array}{c} \mathbf{c} \\ -{z}^* \end{array} \right ] \end{align*}$$
그러면 $\left [ \begin{array}{c} \mathbf{A}^T \\ -\mathbf{b}^T \end{array} \right ], \left [ \begin{array}{c} \mathbf{c} \\ -z^* \end{array} \right ]$에 대해 $(1')$가 거짓이 되어 $(2')$가 참이 된다. 따라서 열벡터 $\mathbf{x} \ge \mathbf{0}$인 스칼라 $\lambda \ge 0$에 대해
$$\newenvironment{bmat}[1]{\left [ \begin{array}{#1}}{\end{array} \right ]} \begin{bmat}{c} \mathbf{A}^T \\ -\mathbf{b}^T \end{bmat}^T \begin{bmat}{c} \mathbf{x} \\ \lambda \end{bmat} = 0, \ \begin{bmat}{c} \mathbf{c} \\ -z^* \end{bmat}^T \begin{bmat} \mathbf{x} \\ \lambda \end{bmat} < 0$$
인데 만약 $\lambda = 0$이라 하면
$$\mathbf{A}\mathbf{x} = \mathbf{0}, \mathbf{c}^T \mathbf{x} < 0, \mathbf{x} \ge \mathbf{0}$$
가 되어 $\mathbf{A}, \mathbf{c}$에 대해 $(2')$가 성립하여 $(1')$이 거짓이 된다. 그런데 그러면 $\mathbf{A}^T \mathbf{y} \le \mathbf{c}$인 $\mathbf{y}$가 존재하지 않아 dual feasibility에 대해 모순이다. 따라서 $\lambda > 0$이다. (여기서 $\lambda$가 원 게시글의 $\alpha$이다. 드디어 $\alpha>0$인 것을 정확히 증명했다!!!)
식을 다시 써보면
$$\mathbf{A} \mathbf{x} = \lambda \mathbf{b} \Rightarrow \mathbf{b} = \mathbf{A} \left ( {1 \over \lambda} \mathbf{x} \right )$$
${\mathbf{x} \over \lambda} \ge \mathbf{0}$ 이므로 ${\mathbf{x} \over \lambda}$는 primal feasible하다. 하지만
$$\mathbf{c}^T \mathbf{x} < \lambda z^* \Rightarrow z^* > \mathbf{c}^T \left ( {1 \over \lambda} \mathbf{x} \right )$$
가 되어 primal optimality가 모순이 된다!
따라서 "dual의 optimal value가 $z^*$보다 작다"는 것은 거짓이 된다. Weak duality와 짬뽕하면
$$ \therefore z^* = \tilde{z}^*$$
로 증명 끝!!!!
Dual Implementation
이제 걱정없이 dual form을 사용해 EMD를 계산할 수 있다. Dual form으로 표현하면 최댓값 $\tilde{z}^* = \mathbf{b}^T \mathbf{y}^*$가 EMD가 된다.
$$ \mathbf{y}^* = \left [ \begin{array}{c} \mathbf{f} \\ \mathbf{g} \end{array} \right ]$$
라고 정의해보자. $\mathbf{f}, \mathbf{g} \in \mathbb{R}^d$이다. 그럼 이건 $\text{EMD} (P_r, P_\theta) = \mathbf{f}^T P_r+ \mathbf{g}^T P_\theta$임을 뜻한다. dual의 제한 조건을 떠올려보자 : $\mathbf{A}^T \mathbf{y} \le \mathbf{c}$
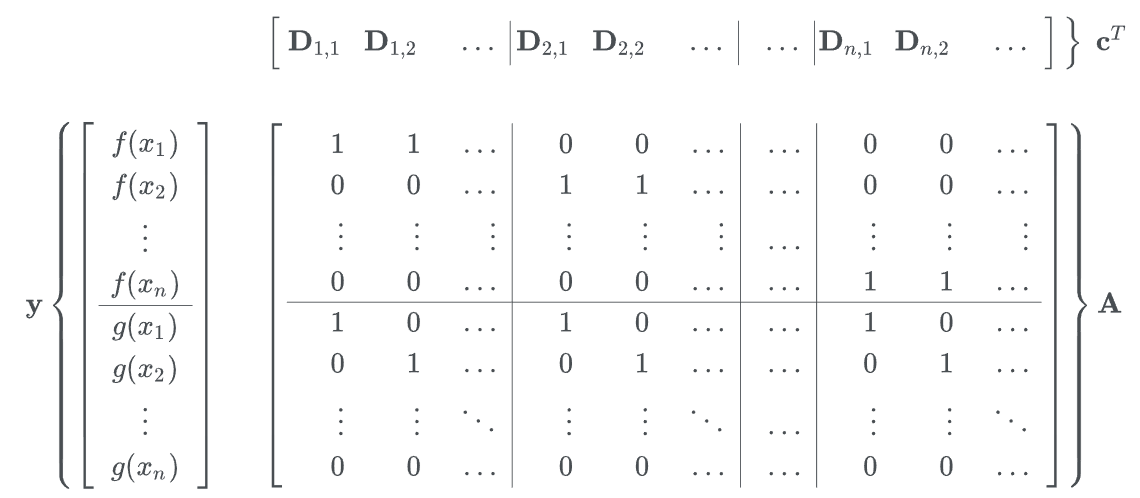
$\mathbf{f}, \mathbf{g}$는 함수 $f, g$의 함숫값들의 벡터이다. $\mathbf{y}$를 $\mathbf{x}$에 대한 함수로 생각한다는 뜻이다. 제한 조건은 $f(x_i) + g(x_j) \le \mathbf{D}_{i, j}$가 되어 state $n^2$개 짜리 $\gamma$ 대신에 길이 $2n$개 짜리 벡터로 표현할 수 있게 됐다.
제한 조건식은 $f(x_i) + g(x_j) \le \mathbf{D}_{i, j}$로 요약할 수 있다. $i =j$인 경우 $\mathbf{D}_{i, i} = 0$이기 때문에 모든 $i$에 대해 $g(x_i) \le - f(x_i)$가 된다. $P_r, P_\theta$가 음이 아니기 때문에 목적 함수가 최대가 되려면 $\sum_i \mathbf{f}_i + \mathbf{g}_i$가 최대한 커야 해서 이 값은 0이고 따라서 $f(x_i) = -g(x_i)$다. 라고 원문에서 그러는데 살짝 비약이 있어서 한 번에 이해가 어렵다. 그래서 그림을 준비했다.

$\left [ \begin{array}{c} P_r \\ P_\theta \end{array} \right ], \left [ \begin{array}{c} \mathbf{f} \\ \mathbf{g} \end{array} \right ]$를 좌표상의 벡터로 나타낼 수 있다.
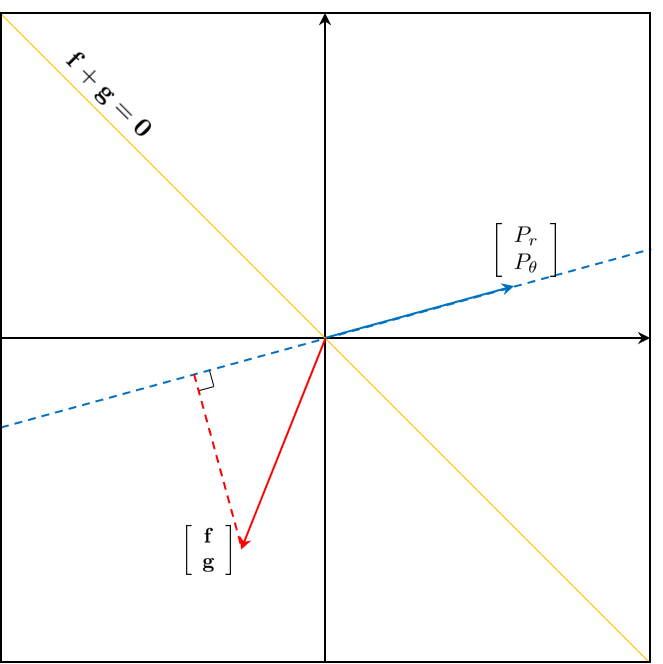
목적함수는 두 벡터 사이의 내적이기 때문에 사영(projection)의 길이가 양수 방향으로 길어질수록 값이 커질 것이다. 만약 $\mathbf{f}$ 또는 $\mathbf{g}$가 무언가에 의해 bounded 된다면 목적함수가 최대가 되게 하는 $\left [ \begin{array}{c} \mathbf{f} \\ \mathbf{g} \end{array} \right ]$는 $\mathbf{f} + \mathbf{g} = \mathbf{0}$위에 존재하게 된다.
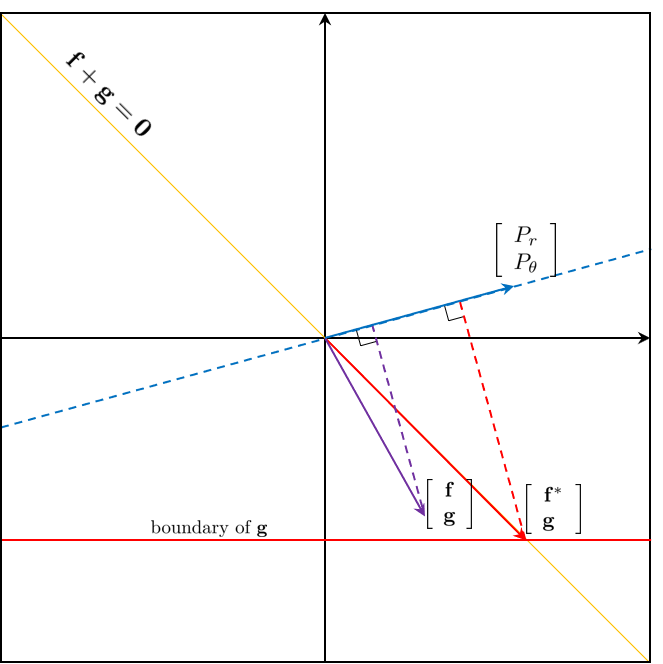
하지만 무엇이 $\mathbf{f}, \mathbf{g}$를 bound 시킬까? 바로 $f(x_i) + g(x_j) \le \mathbf{D}_{i, j}$ 조건이다. 따라서 목적함수가 최대가 될 때 $\mathbf{g} = -\mathbf{f}$이다. 이를 다시 원래의 제한조건에 대입하면 $f(x_i) - f(x_j) \le \mathbf{D}_{i. j}$ 그리고 $f(x_i) - f(x_j) \le \mathbf{D}_{i, j}$를 만들 수 있다. ($i$와 $j$를 바꾸면 된다.) 만약 $f(x_i)$가 연속적으로 이어져있다고 생각하면 함수의 평균변화율이 $-1$과 $1$로 bounding되는 것을 알 수 있다. 이런 함수를 립쉬츠 함수라고 하며 $\pm 1$에 의해 bounding 되었으므로 1-립쉬츠 함수라고 한다. 수식으로 $||f||_{L \le 1}$로 나타낸다. 따라서 EMD는
$$\text{EMD}(P_r, P_\theta) = \sup_{||f||_{L \le 1}} \mathbb{E}_{x \sim P_r} [f(x)] - \mathbb{E}_{x \sim P_\theta} [f(x)]$$
가 된다.
'수학' 카테고리의 다른 글
| Mathematics | MLE vs. MAP vs. Bayesian (3) | 2022.12.17 |
|---|---|
| Mathematics | Fourier Analysis | Basic Properties of Fourier Series (2) | 2021.08.14 |
| Mathematics | Information Theory | Entropy, Information (0) | 2021.08.13 |
| Mathematics | 왜 하필 Borel Set일까? (1) | 2019.03.21 |



