이전 글에서 이어진다.
[Mamba 이해하기 1-1] HiPPO의 A 행렬의 중요성 | HiPPO: Recurrent Memory with Optimal Polynomial Projections, Gu et al.
다루고자 하는 문제: 시계열 모델링1차원 연속 신호 $x(t)$가 주어졌을 때, 우리가 원하는 종류의 신호 $y(t)$로 바꿔주는 함수(또는 시스템) $f(t): \mathbb{R}_+ \rightarrow \mathbb{R}$을 찾는 문제이다. $x(t)$
haawron.tistory.com
Task: Online Function Approximation
Online function approximation은 매 time step $t$마다 함수 $f$의 $x \le t$ 부분을 완전히 기억하는 것을 목표로 한다. 정의역이 $x \le t$로 제한된 함수 $f$를 $f_{x\le t}$ 또는 $f_{\le t}$로 표기한다.
HiPPO는 $f_{\le t}$를 고차 다항함수의 합으로 표현하려고 한다. 정확히는 $N$차 다항함수 $N$개 $p_0^{(t)}, p_1^{(t)}, \dots, p_{N-1}^{(t)}$를 미리 정의해놓고 $f_{\le t}$를 가장 잘 표현하는 다항 함수의 선형결합의 계수들 $c_n(t)$를 구하려고 한다. 이를
$$f_{\le t} \approx \sum_{n=0}^{N-1} c_n(t) p_n^{(t)}$$
와 같이 표현 할 수 있다. 따라서 HiPPO는 임의의 실함수 $f$를 고차 다항함수(High-order Polynomial)로 재표현(Projection)하는 연산자(Operators) 또는 그 프레임워크를 일컫는 말이다.
내가 생각하는 Contributions
1. 장기 기억 모델 HiPPO 제시: 기존 RNN, LSTM, GRU 등의 시계열 모델 연구의 핵심은 explicit한 기억과 망각이다. 기억, 망각 회로를 직접적으로 집어넣어 모델이 시계열 데이터의 특정 부분을 얼마나 기억하거나 잊게 할지 결정하도록 한다. 한편, 다항함수는 계수 $N$개만으로도 함수 전체를 복원할 수 있다. 따라서 유한 개의 스칼라로 거의 완벽한 암기를 할 수 있다. 기억 회로에 HiPPO를 바꿔 끼워 넣음으로서 시간 거리가 먼 곳도 참조(long-term dependency)할 수 있게 된다.
2. 실시간 문제를 빠르게 푸는 법 제시: 실시간이 아닌 다항회귀는 이미 연구가 많이 된 분야이지만 실시간 피팅으로 넘어와서는 재밌는 목표를 세운다. 바로 이전 time step의 결과를 재활용 할 수 있지 않을까 하는 것이다. 맞추고자 하는 함수는 변하지 않으므로 충분히 가능한 목표이다. 실제로 $K$개의 점이 주어졌을 때, $N$차 다항회귀 방법의 시간복잡도는 $O(K\cdot N^2 + N^3)$이다. 역함수 연산에 따라 달라지긴 하지만 $K$는 매우 크다. 따라서 함수 차원 $N$은 심각한 제한을 받는다. 하지만 HiPPO는 이전 결과를 재활용하여 빠르게 푸는 법을 제시하면서 매우 큰 $N$ 값을 가져갈 수 있다.
3. HiPPO가 LSTM, GRU 등의 generalization임을 수학적으로 보임: 특정한 다항함수 집합을 활용하면 LSTM, GRU를 도출할 수 있다.
4. HiPPO의 4가지 특징 발굴: 2번을 포함하여, 시간 스케일에 영향 안 받음, RNN에 삽입되면 gradient vanishing 문제 해결 가능, 에러값 상계의 4가지 특징이 존재하고 appendix에 증명이 돼있다. 2번과 시간 스케일에 영향을 안 받는다는 내용이 가장 중요하다. 10Hz로 학습한 모델에게 20Hz 인풋을 넣어줘도 똑같은 성능이 나온다는 뜻이다.
논문 읽다가 막히는 부분들, 이 글의 목표
논문의 본문에는 최대한 수학적인 요소를 빼려고 한 것 같지만 수학적인 요소가 빠지니 반만 이해된 느낌이 든다. 예를 들면
- $\mu$는 내가 맘대로 설정할 수 없나?
- 왜 Time-scale에 invariant 한가?
- 왜 빠른가?
- 대체 $A$는 어디서 나왔나?
- HiPPO를 응용하려고 할 때 건드리면 안 되는 부분은 어디인가?
- Interpretable 한가?
등의 왜 질문들이 있을 것이고
- GBT
- Measure, dot product
- SSMs
- $c$는 뭐고 $c{(t)}$는 뭐고 $c_n{(t)}$는 뭐고, 얘를 $t$로 미분...?
등의 개념적인 질문들이 있을 것이다. 이 글에선 위 질문들을 모두 해결하는 것을 목표로 한다.
HiPPO
HiPPO 프레임워크는 3부분으로 나뉜다. $\text{proj} _t$, $\text{coef}_t$, discretize이다. 시간에 따른 다항함수 계수들의 변화를 SSM으로 표현하여 재활용하는 구조다. SSM과 measure에 대해 잠깐 알아보고 각 연산자를 하나씩 알아볼 것이다.
SSMs; State-Space Models
공학의 많은 문제에서 미분방정식(ODE; Ordinary Differential Equation)이 등장하게 된다. 보통 시간에 따른 인풋 함수 $f_i(t)$와 상태함수 $f_\text{state}(t)$, 원하는 정보인 아웃풋 함수 $f_o(t)$로 구성되어있다. 미분방정식은 보통 여러 개가 동시에 등장한다. 이들을 잘 정리하면 인풋, 아웃풋, 상태의 관계를 행렬로 표현할 수 있다. ODE의 행렬 표현이 SSM인 것이다.
미분방정식 여러 개를 행렬로 표현할 수 있다는 내용과 미분방정식의 이산화(discretize)에 대한 내용을 들고 갈 것이다.
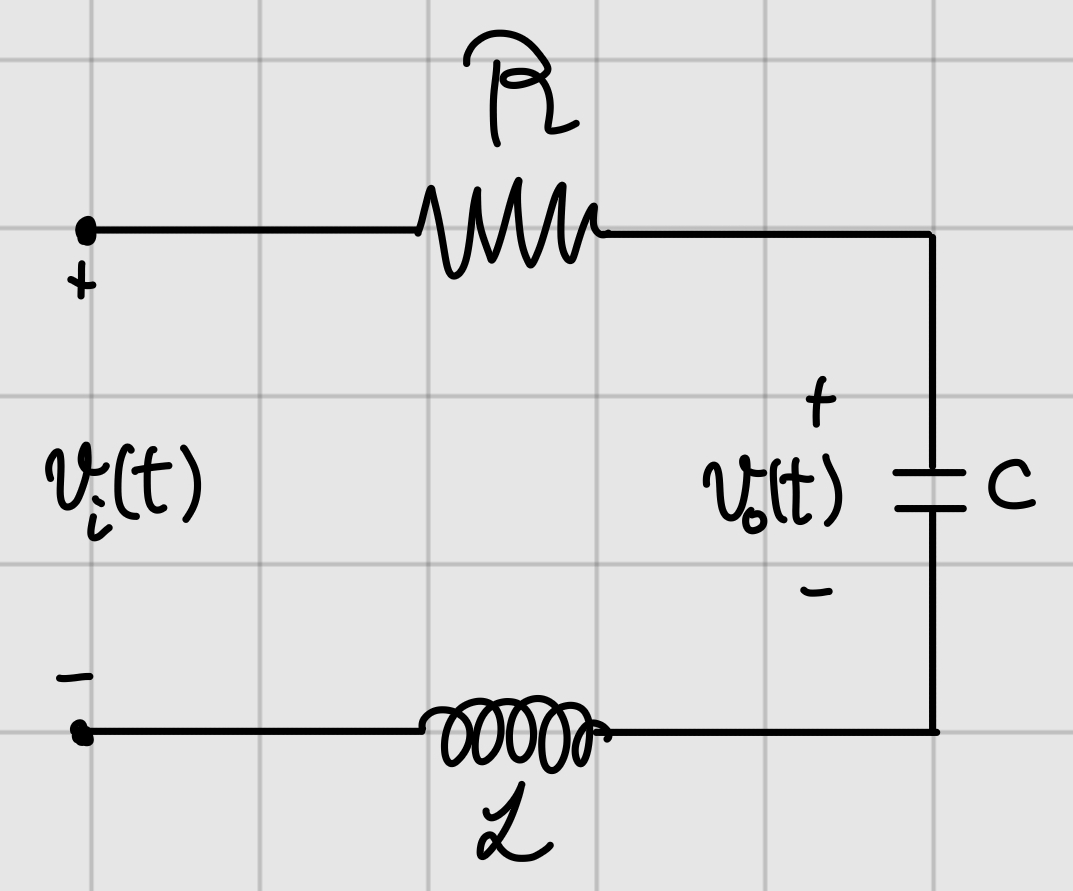
ODE까지는 많이 접해봤어도 SSM은 생소할 수 있다. 나는 SSM을 4학년 자동제어를 와서야 배웠다. 친근한(?) ODE로부터 SSM을 만들어보자.
위는 전자공학에서 등장하는 SSM의 한 예시이다. 간단한 RLC 회로이다. 기계공학에서는 질량-스프링-댐퍼 모델에 대응된다. 인풋은 시간에 따른 전압 $v_i$이고 우리는 캐패시터에 걸리는 전압 함수 $v_o$를 구하려고 한다. 이를 위해 전류 $i$를 상태로 사용한다. $R, L, C$는 저항, 인덕터, 캐패시터의 저항값, 인덕턴스, 캐패시턴스를 의미한다. 상수값이다.
조금만 더 설명하자면 옴의 법칙에 따라 저항에 걸리는 전류, 전압은 $V=IR$의 비례 관계를 가질 수 있다. 인덕터, 캐패시터의 것들은 미분방정식으로 표현된다.
$$v=L\frac{\text{d}i}{\text{d}t} \ , \quad i = C\frac{\text{d}v}{\text{d}t} \ .$$
그리고 위 회로에서 소자들의 전류값은 모두 같다.
서론이 길었지만 이들의 관계를 아래 두 식으로 정리해서 표현할 수 있다.
$$\begin{align*}
\frac{\text{d}i}{\text{d}t} &= - \frac{R { \color{red}{i} } }{L} - \frac{ \color{red}{v_c} }{L} + \frac{ {\color{blue}{v_i}} }{L} \\
\frac{\text{d} v_c}{\text{d}t} &= \frac{i}{C}
\end{align*}$$
멀리서 보면 뭔가 $v_i$를 인풋으로 집어넣으면 $i, v_c$가 이를 인코딩하는 구조 같다. 그리고 선형이다! (제곱이나 나누기 같은 것들이 없다.) 따라서 행렬로 표현할 수 있다.
열심히 정리하면 위와 같이 된다. 쓸데없이 복잡하게 표현한 것 같아도 generalization 하기 편하기 때문에 분석에 다양한 아이디어를 활용할 수 있다. 식들을 유심히 보면 아래와 같이 정리할 수 있다.
SSM이 완성되었다. $u$를 입력, $x$를 상태, $y$를 출력이라고 한다. $A$는 상태천이행렬(transition matrix)이다. SSM은 상태가 어떻게 바뀌는지 분석하기 위해 만들어진 모델이기 때문에 $A$가 가장 중요하다. $A$의 고윳값, 고유벡터 등을 분석하여 시스템의 특성을 미리 알 수 있다. 진동할지 발산할지 파형에 굴곡이 몇 개일지가 그 예이다. 이러한 시스템의 행동양상을 dynamics라고 한다.
자동차 시트를 예로 들면 과속방지턱을 넘을 때 우리 몸은 진동을 2번 정도 느낀 후 정지한 느낌을 받는다. SSM으로 진동 2번을 예측할 수 있다. $A$의 고윳값은 $R = 2\sqrt{L/C}$이면 입력 전압이 갑자기 가해졌을 때(step function) 출력이 무한히 진동할 것이라고 알려준다.
요약하면, ODE가 선형적으로 표현된다면 SSM을 만들 수 있고, 여기서 나온 $A$는 상당히 많은 정보를 알려준다.
SSM과 ODE의 이산화(Discretization)
문제를 컴퓨터로 푼다면 함수가 아닌 함숫값들이 이산적으로 주어진다. 시간 간격 $\Delta t > 0$에 대해 $u[k] = u(k\Delta t), k \in \{0, 1, \dots\}$에 대한 상태 수열 $x[k]$를 이산화를 통해 도출할 수 있다. 미분의 정의부터 시작한다.
$$y'(t) = \lim_{\Delta t \rightarrow 0} \frac{y(t+\Delta t) - y(t)}{\Delta t} \ .$$
만약 시간 간격 $\Delta t$가 충분히 작다면 다음과 같이 표현할 수있다.
$$ y'(t) \approx \frac{y(t+\Delta t) - y(t)}{\Delta t} \ .$$
그리고 정리하면,
$$ y(t + \Delta t) \approx y(t) + \Delta t y'(t) $$
$$ y(t + \Delta t) - y(t) \approx \Delta t y'(t) $$
$$ y[k+1] - y[k] \approx \Delta t y'(t) $$
와 같이 표현된다. 보통 미분방정식은 $y'(t) = f(t, y)$ 형태로 주어진다. 매 time step $ t = k \Delta t $마다 $f(t, y)$는 대입만으로 쉽게 얻을 수 있으므로 차분값을 구해 미분방정식을 차분방정식으로 바꿀 수 있다. 이 과정이 이산화이며, 방금 소개한 방법은 forward Euler method라고 한다.
(TODO: Bilinear와 GBT는 나중에 소개하겠다.)
위키피디아에서 많은 부분을 참조했다.
Measure와 함수 간 내적
우리는 함수 $f_{\le t}$의 가장 비슷한 다항함수 전사(projection) $g^{(t)}$를 구하고싶다. 여기서 '비슷한'을 정의하기 위해 거리 개념이 필요하다. 함수를 벡터의 연장으로 생각해서 RMSE를 거리로 두면 되지 않을까? 하는 생각이 들 수도 있다. 어느 정도 맞다.
$[0, \infty)$에서 정의된 실함수 $f, g$가 square integrable이라면 내적 $\langle f, g \rangle_{L_2} = \int_0^\infty f(x)g(x)\text{d}x$는 힐베르트 공간을 형성할 수 있고, $f$의 norm은 $\lVert f \rVert_{L_2} = \langle f, f \rangle_{L_2} ^{1/2}$와 같다.
여기서 square integrable은 적분 $\int_0^\infty |f(x)|^2 \text{d}x$가 발산하지 않는다는 뜻이고, 힐베르트 공간은 함수들의 집합인데 이 공간의 함수들은 내적값이 크면 비슷하게 생겼다는 것을 알려준다. 거리는 $\lVert f - g \rVert_{L_2}$로 정의할 수 있다.
한편, 우리는 함수를 다항함수로 표현하고 싶다. 만약 다항함수들이 orthogonal basis를 형성한다면 예쁘게 표현할 수 있겠다.
(잠깐 선형대수 복습: 기저(Basis)?)
우리는 선형대수에서 $N$차원 벡터 $u$를 orthogonal basis $\mathcal{V} = \{v_0, v_1, \dots, v_{N-1}\}$이 span하는 선형공간에 전사를 시켜봤다. 다항함수간 전사를 이해하기 위해 이미 배운 내용에서 analogy를 갖고 갈 것이다.
$$ \begin{align*}
u \approx \hat{u} &= c'_0 v_0 + c'_1 v_1 + \cdots + c'_n v_n + \cdots + c'_{N-1} v_{N-1} \\
&= \sum_{n=0}^{N-1} c'_n v_n
\end{align*}
$$
이를 $ \hat{u} $의 basis expansion이라고 한다. 기저가 orthogonal 하다는 뜻은 임의의 $i, j \in [N]$에 대해 $\langle v_i, v_j \rangle = \delta_{ij}$라는 뜻이다. 따라서 계수 $c'_n$은 내적으로 쉽게 구할 수 있다.
$$ \begin{align*}
\langle \hat{u}, v_n \rangle &= \left \langle \sum_{i=0}^{N-1} c'_i v_i \ , \ \ v_n \right \rangle \\
&= \sum_{i=0}^{N-1} c'_i \langle v_i, v_n \rangle \\
&= 0 + 0 + \cdots + c'_n \langle v_n, v_n \rangle + \cdots + 0 \\
&= c'_n \lVert v_n \rVert ^2 \\
&=: c_n \ .
\end{align*}$$
다시 돌아와서, 우리는 내적이 잘 정의됐다면 $N$개의 orthogonal한 다항함수 기저도 정의할 수 있다는 사실을 알게 됐다. (많은 게 생략됐지만 맥락은 비슷하다.) 임의의 두 다항함수를 곱해서 적분했을 때 0이 나오는 다항함수 집합을 찾으면 된다. 조금 어렵지만 이미 정의된 유명한 orthogonal한 다항함수 기저들이 많다. 라게르, 르장드르 다항함수가 그 예이다. 정확히는 내적을 위와같이 정의하면 안 되고 적절한 weight function $w(x)$를 같이 줘야 수직이 된다.
"적절한 $w(x)$를 줬다"는 것을 $\text{d}\mu(x)$로 표현한다. 그러면 정의가 아래와 같아진다.
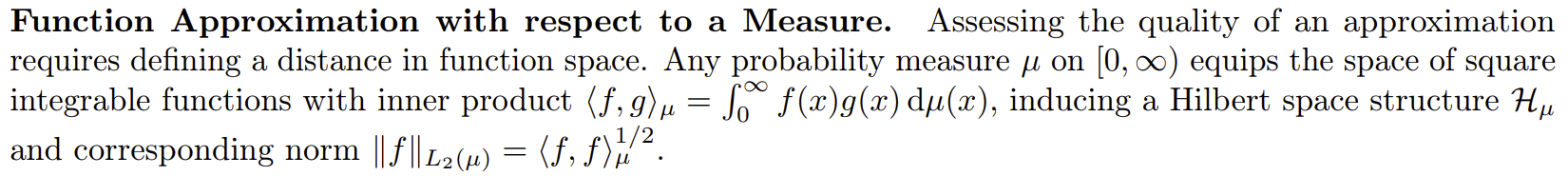
여기서 적절한 weight function을 주는 $\mu$를 측도(measure)라고 한다. 측도는 내맘대로 정의하면 안 된다. 선택한 다항함수 기저를 orthogonal하게 만들 수 있도록 줘야 한다. 라게르를 예를 들면 $w(x) = x^\alpha e^{-x}, x \ge 0$을 줘야 한다. 다항함수 기저를 고르면 적절한 측도는 알아서 정해진다. (르장드르의 경우는 $w(x)=1/2$이다. 특별한 측도가 없어도 orthogonal이다.)
한편, HiPPO에서는 이렇게 정해진 측도를 '시간에 따른 중요도'로 해석했다. 라게르 weight function에서 $\alpha = 0$으로 주면 $w(x) = e^{-x}$가 된다. HiPPO에서는 이를 뒤집고 translate 해서 $e^{-(t-x)}, x \le t$로 만들었다. $x$가 $t$에서 멀어질수록 기하급수적으로 값이 작아진다. 이를 "오래됐을수록 기하급수적으로 덜 중요하다"라고 해석하는 식이다.
논문에서는 측도를 먼저 주면 다항함수가 따라오는 것처럼 표현이 돼서 혼란을 야기한다. 실상은 적절한 다항함수 기저를 먼저 골라놓고 이를 orthogonal 하게 만들기 위해 준 측도들이 time-domain에서 reasonable 하게 해석이 된 것이다.
$\text{proj}_t$와 $\text{coef}_t$와 계수들의 Dynamics
우리는 $f_{\le t}$를 다항함수 $g^{(t)}$에 전사시키고 있다. $g^{(t)}$는 orthogonal한 다항함수 기저 $\{g_n\}_{n < N}$이 span하는 공간의 한 원소이다. $g^{(t)}$의 basis expansion의 계수 $c_n(t)$는 내적으로 쉽게 구할 수 있다. 논문에서는 아예 내적으로 정의해버렸다.
$$f_{\le t} \approx g^{(t)} \\c_n(t) := \langle f_{\le t}, g_n \rangle_{\mu^{(t)}} \ . $$
위가 전사$\text{proj}_t$, 아래가 계수 구하기$\text{coef}_t$ 연산이다.
한편, 구한 계수들을 실시간으로 재활용하려면 계수들의 dynamics를 활용할 수 있다. Dynamics는 SSM을 구하면 쉽게 알 수 있다. SSM을 구하려면 ODE를 먼저 closed-form으로 구해야 한다. $c_n(t)$의 정의로부터 closed-form ODE를 얻으려면 어떻게 해야 할까? 우리가 원하는 form은
$$ c'_n(t) = [ \text{function of } c_n(t) \text{ and } t ] $$
이다. 공교롭게도 함수간 내적은 적분으로 정의된다. 그럼 $c_n(t)$의 정의를 미분하면? 좌변은 우리가 원하는 폼이 되고 우변은 계산을 조금만 거치면 $c_n(t), c_{n-1}(t), \dots$와 $t$로 표현할 수 있다. 다만 계산이 조금 복잡해서 appendix로 갔다. 우리는 연산자 정의만 살펴보고 appendix로 넘어갈 것이다. 맛을 잠깐 먼저 보자면,
이렇게 생겼다. 계산은 저자가 다 해놨으니 우리는 차근차근 따라가기만 하면 된다.
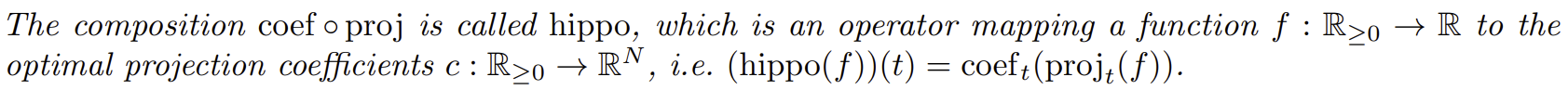
$\text{hippo}(f)$의 결과는 전사된 함수의 basis expansion의 계수인 $N$개의 스칼라이며, 그 계수는 매 시간 $t$마다 바뀐다. 왜냐하면 연산자들이 매 시간 $t$마다 바뀌기 떄문이다. 연산자가 바뀌었다는 뜻은 같은 인풋에 대해 다른 아웃풋을 내놓는다는 것이다. 실시간으로 연산자들이 바뀌는 이유는 $\mu^{(t)}$가 바뀌기 때문이다! 여기부터 어지럽다. Appeindix에서 머릿속의 빈공간을 채워보자.
Appendix 톺아보기
우리는 Appendix의 C와 D를 알아볼 것이다. C는 $f$로부터 $c$를 얻는 과정을 제너럴하게 설명하고, D는 scaled and shifted 르장드르 다항함수 기저와 측도(LegS)를 대입해서 직접 계산한다. D에서는 LegS말고도 여러 기저-측도 세트에서도 계산을 했지만 우리는 LegS만 살펴볼 것이다
Appendix C는 문제 정의부터 시작한다. $(-\infty, t]$에서 정의된 time-vaying measure $\mu^{(t)}$, 기저 함수 수열이 만드는 공간 $\mathcal{G} = \text{span} \{ g_n^{(t)} \}_{n \in [N]}$와 연속함수 $f: \mathbb{R}_{\ge 0} \rightarrow \mathbb{R}$ 가 주어졌을 때, HiPPO는 $f$로부터 다음을 만족하는 $f$의 optimal projection의 계수 $c: \mathbb{R}_{\ge 0} \rightarrow \mathbb{R}^N$를 얻는 연산자로 정의한다.
HiPPO라는 상자에 $f$를 넣으면 $c$가 나온다!
우리는 이로부터 ODE $\frac{d}{dt}c(t) = Ac(t)+Bf(t),\in\mathbb{R}^{N\times N}, B \in \mathbb{R}^{N\times 1}$를 얻을 것이다.
C.1 각종 정의들
시간에 따른 중요도인 측도 $\mu$가 주어졌을 때 $\{ P_n \}_{n \in \mathbb{N}}$은 $\mu$에 대해 orthogonal 한 다항함수 기저로 정의한다. $\langle P_i, P_j \rangle_{\mu} = \delta_{ij}, i, j \in \mathbb{N}$이 된다는 뜻이다. 논문에서는 이렇게 써놨지만 실상은 순서가 반대다. 체비셰브, 라게르, 르장드르 같은 유명한 다항함수 기저를 먼저 채택하고 이들을 orthogonal하게 만드는 $\mu$를 찾는 것이다.
한편 실시간 다항회귀에서는 실시간으로 정의역이 변한다. 시점 $t$에서 $[0, t)$이다. $\mu$는 정의역 전체를 커버해야하기 때문에 $\mu$도 같이 변한다. 이를 $\mu^{(t)}$로 표기한다. 다항함수는 측도랑 세트기 때문에 같이 변한다. 함수꼴이 변하는 건 아니고 간단한 scaling and shifting 정도만 한다. 이를 $\{ P_n ^{(t)} \}_{n \in \mathbb{N}}$으로 표기한다.
$p_n^{(t)}$는 $P_n^{(t)}$의 normalized 버전이다. Norm이 1이 되도록 norm으로 나눠준 것이다.
$$ p_n(t, x) = p_n^{(t)}(x) $$
로 정의한다. 그때그때 저자가 좀 더 명확하다고 생각하는 표현으로 바꿔 쓴다. 위키피디아 같은 곳에 정의된 $P_n^{(t)}$는 normalized 될 필요는 없다. 해당 논문에서는 $p_n^{(t)}$를 주로 사용한다.
여기에 tilting이라고 다항함수를 orthogonal로 만들어주기위한 장치가 하나 더 있는데 르장드르는 필요 없기 때문에 정의는 생략한다. 다만, 계속 등장하기 때문에 르장드르에서는 $\chi=1$, $\zeta = 1$, $g_n = p_n$, $\nu = \mu$라고 생각해서 대입하면 된다.
그리고 $\omega(t, x) = \omega^{(t)}(x)$는 $\mu$가 주는 중요도 weight function이다.
C.2 전사와 계수
인풋은 실시간(online)으로 주어지는 $f$의 일부분(제한; restriction) $f_{\le t}(x) = f(x)_{x \le t}$이다. $f: [0, \infty) \rightarrow \mathbb{R}$는 1번 이상 미분 가능한 함수이다.
아웃풋은 최적의 전사의 계수이다. orthogonal basis $\{ p_n \}_{n \in [N]}$이 주어졌을 때,
$$ \begin{align*}
c_n(t) &:= \langle f_{\le t}, g_n^{(t)} \rangle_{\mu^{(t)}} \\
&= \int fp_n^{(t)} \omega^{(t)} \\
&= \int_{0}^t f(x) \cdot p_n^{(t)}(x) \cdot \omega^{(t)}(x) \text{d}x
\end{align*}$$
로 계산한다. $c$의 정의이다. 아래에서 길을 잃으면 보통 얘 때문이다. $c$가 뭐지..? 하는 생각이 들면 여기로 다시 오면 된다.
계수를 구했으면 함수를 복원(reconstruct)할 수 있다.
$$ f_{\le t} \approx g^{(t)} := \sum_{n=0}^{N-1} \langle f_{\le t}, p^{(t)}_n \rangle_{\mu^{(t)}} = \sum_{n=0}^{N-1} c_n(t)p_n^{(t)} $$
로 계산한다. 이 글 첫 움짤의 초록색이 $g^{(t)}$이다. 바로 위 식이 $\text{proj}_t$의 실체이다. $\text{coef}_t$는 여기서 $c$만 뽑아가는 연산자이다.
C.3 Coefficient Dynamics
위 내적으로부터 ODE를 만들어볼 것이다. $t$로 미분한다.
$$ \begin{align*}
\frac{d}{dt} c_n(t) &= \int f(x) \left ( \frac{\partial}{\partial t} p_n (t, x) \right ) \omega(t, x) \text{d}x \\
&+ \int f(x) p_n(t, x) \left ( \frac{\partial}{\partial t} \omega(t, x) \right ) \text{d}x
\end{align*} $$
고등학교 때 배운 곱의 미분의 확장이다. 우변을 $c$와 $t$로 다시 표현하는 것이 핵심이다. 첫 번째 항부터 보면, 다항함수는 미분해도 다항함수고 기저에서 벗어나지 않는다. 따라서 $p_0, \dots, p_{n-1}$의 선형결합으로 표현할 수 있다. 그럼 $c$로 다시 표현할 수 있다.
두 번째 항이 문제이다. $\omega$가 미분했을 때 이상한 form이 나오면 적분이 그대로 살아있을 거기 때문에 여기서 막힌다. 하지만 르장드르의 경우 $\omega'$도 $\omega$로 다시 표현이 가능하다. 따라서 $c$의 정의에 따라 $c$로 다시 표현이 가능하다.
따라서 ODE가 완성된다. 완성된 ODE는 D에서 확인한다. 그렇다면 ODE를 다음과 같이 정리할 수 있을 것이다.
$$ \frac{d}{dt} c(t) = -Ac(t) + Bf(t) \ .$$
이게 $\text{hippo}$ 연산자의 실체이다. $A$앞의 $-$부호는 계산의 편의를 위해 해놓았다.
C.4 이산화
$ \frac{d}{dt} c(t) = -Ac(t) + Bf(t) $로부터 $c_k = -Ac_{k-1} + Bf_k$를 얻는다.
D. HiPPO 연산자 계산
대망의 D이다. D는 C에서 유도한 식에 각 다항함수 기저와 측도를 대입한다. 우리는 LegS만 살펴볼 것이다. 계산은 4단계이다. 1. 측도와 기저, 2. 다항함수 미분, 3. 계수 동역학, 4. 복원.
1. 측도와 기저
르장드르 다항함수 $P_n$은 $[-1, 1]$에서 정의된다. $[0, t]$에서 사용하려면 위와 같은 약간의 scaling을 거쳐야 한다. $(2n+1)^{\frac{1}{2}}$는 $P_n$의 norm이다. $\mathbb{I}$는 rect function이다. $[0, t]$에서만 1이고 나머진 전부 0이라는 뜻이다.
오른쪽 그림의 파란색, 보라색은 서로 다른 $t$에 대한 $\omega$이다. 이 그림이 이해된다면 넘어가도 된다.
2. 다항함수와 중요도 함수 미분
적분꼴을 없애려면 $\omega'$는 $\omega$로, $g'$은 $g$로 표현하는 것이 핵심이다. ($c$의 정의를 다시 보고 오면 된다.)
여기서 $z = \frac{2x}{t} - 1$로 놓으면,
가 된다. $g_n, g_{n-1}, \dots$로 재표현 됐다.
3. 계수 동역학
C.3에서 만든 식에 2.에서 계산한 미분 식을 대입하면 된다.
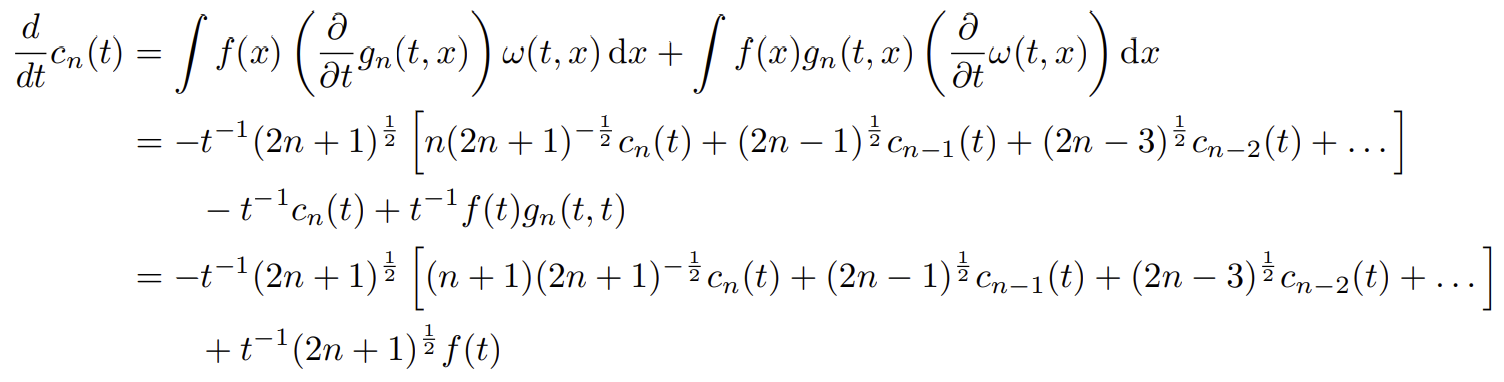
선형결합이기에 아래와 같은 행렬 표현이 가능하다.
여기 $A$가 이제 계속 등장할 HiPPO-LegS $A$이다. $A$앞의 $-$ 부호에 주의한다.
4. 복원
이산화
위 GBT 계산 식에 집어넣으면 된다. 이마저도 미리 계산되어있다.
$$ c^{(k+1)} = \left ( I - \frac{1}{k+1} \alpha (-A) \right ) ^{-1} \left ( I + \frac{1}{k}(1 - \alpha)(-A)\right ) c^{(k)} + \frac{1}{k} \left ( I - \frac{1}{k+1} \alpha (-A) \right ) ^{-1} B f_k $$
논문에서는 $A$의 $-$가 고려 안 된 상태로 표기되어 있어 혼동을 유발한다. 구현을 위해 식 하나로 표기했다.
여기서 핵심은 HiPPO-LegS의 이산화는 $\Delta t$가 없다는 점이다. 다 자기끼리 나눠져서 없어진다. 따라서 time-scale에 invariant 하다.
코드
르장드르 다항함수는 기본적으로 계수들이 매우 작기 때문에 sympy 기반의 `Legendre` 클래스를 사용해 연산을 먼저 하고 함숫값은 나중에 eval 한다.
`A_bwd`를 계산할 때 $\frac{1}{k+1}$을 넣으면 값이 튄다. $\frac{1}{k}$를 넣었다.
문제점
아직 HiPPO가 완성되지 않았다. HiPPO의 큰 장점 중 하나는 $N$에 선형인 연산 속도이다. 반면 위의 이산화 식을 보면 $O(N^3)$을 요구하는 역함수가 껴있다. 여기서도 저자의 천재성이 드러난다. 천재적인 방법으로 불필요한 연산을 줄였다.
'AIML' 카테고리의 다른 글
| [Mamba 이해하기 1-1] HiPPO의 A 행렬의 중요성 | HiPPO: Recurrent Memory with Optimal Polynomial Projections, Gu et al., NeurIPS 2020 (0) | 2024.09.03 |
|---|---|
| [Mamba 이해하기 0] 개요 (0) | 2024.09.03 |
